10＋1 website｜テンプラスワン・ウェブサイト

建築を情報の観点から再定義しその体系化を目指す建築情報学会。その立ち上げのための準備会議が開催されている。「10＋1 website」では、全6回にわたってこの準備会議の記録を連載。建築分野の内外から専門的な知見を有するゲストを招き、建築情報学の多様な論点を探る。連載第5回は、新井崇俊氏がモデレーターを務め、「エンジニアド・デザイン」と題してデザインへの工学的アプローチの方法を議論する。

- 本記事は、当日の記録をもとにキックオフグループメンバー（池田靖史氏、豊田啓介氏、新井崇俊氏、石澤宰氏、木内俊克氏、角田大輔氏、堀川淳一郎氏）による事後的な注釈（☆印）を付している。
- 準備会議に先んじて、メンバーによる対談と論考を「特集＝建築情報学へ」に掲載している。本連載と併せて参照されたい。

−

1. 登壇者プレゼンテーション

1.1. 新井プレゼンテーション

新井崇俊──私は東京大学生産技術研究所で建築・都市計画の研究をしている傍ら、hclab.というグループでも、都市解析や建築設計の活動をしています。今日は、ゲストスピーカーとしてdoubleNegatives Architecture主宰の市川創太さんと、東京大学空間情報科学研究センターの本間健太郎さんに来ていただきました。お二人とは研究と設計で一緒に活動しており、普段から問題意識を話し合っています。今日は、コンピュテーショナルに建築や都市をデザインすることで一体何ができるのか。会場のみなさんと一緒に掘り下げていきたいと思っています。

新井崇俊氏

建築デザインの分野では、一般的にデジタル技術を応用したアプローチ、とりわけRhinoceros＋Grasshopperを使うことを「コンピュテーショナルデザイン」と呼ぶことが多いと思います。しかし私は、特定のアプリケーションに限らず、コンピュータを利用したデザインすべてが「コンピュテーショナルデザイン」だと考えています。

これを深掘りするために、今日はテーマとして「エンジニアド・デザイン」というタイトルをつけました☆1。これは私の造語です。建築デザインへの工学的アプローチによるコンピュテーショナルデザイン、より具体的に言えば、再現性のあるプロセスを経た計算可能なデザインを「エンジニアド・デザイン」と呼んで☆2、お二人とディスカッションしたいと思っています。

☆1──［豊田］「エンジニアド・デザイン」という言葉は、提供される解がそれ自体すでにいろんな条件や関係性の結果であるというように、解自体が動的な条件を含んでいる新しいデザインのパラダイムを、すごく端的に表現していると思う。
☆2──［木内］非常に明快な定義で、「再現性のあるプロセス」という部分の目的性についてとても考えさせられた。「再現性」は「可読性」でもある。読めることは意味を担保する作用を生み、メタな次元で建築をコミュニケーションする媒体にもなっている。

そもそも、工学的アプローチと科学的アプローチは何が違うのか。私はそれぞれの目標が違うと理解しています。科学（サイエンス）の目標は「世界を解明すること」だとすれば、工学（エンジニアリング）の目標は「世界を改善すること」だと思います。もちろん、この両者は重なる部分もあれば、そうでない部分もあります。

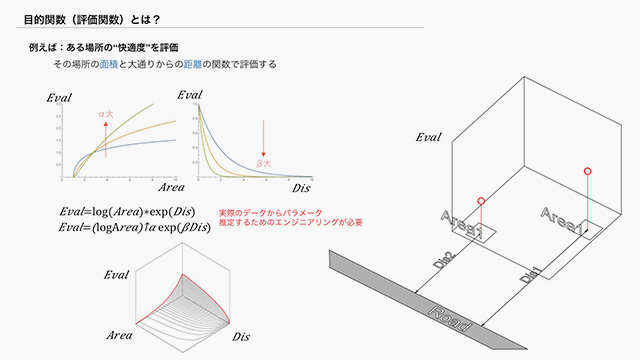
例えて言うと、物体に加わる力とトルクにどのような関係が成り立つかを示して見せるのが科学だとすれば、工学はその関係を用いて、可能な限り高速で移動できる、あるいはエネルギー効率の高いエンジンなどをつくるためにどうすればいいのかを考える学問だと思います。この例の場合、移動時間や消費電力などを表す関数を設計し最小化することになりますが、この関数を工学の分野では「目的関数（評価関数）」と呼ぶことが多いです☆3。

☆3──［豊田］デザインという領域でこそ、これからは評価関数やパラメータ、有効数字や有効なスケールや領域、それらの分析をロジカルに考える技術や感覚がとても重要になってくる、と最近特に感じている。感覚の世界だからこそ、こういうものとより高次な補完関係を築きうる時代。

今度は、ある空間の快適度を評価する例を考えてみましょう。まずシンプルに空間の面積（広いほど快適）と、大通りからの距離（騒音などの影響で近いほど不快）の2値で快適度が表されるとしましょう。さらに、面積に対しては対数的に、距離に対しては指数的に快適度が変化すると仮定し、その積で快適度を評価してみます☆4［fig.1-1］。しかし、（広いほど快適）（大通りから近いほど不快）という関係には、増加や減衰の「程度」があるので、それぞれに対してパラメータを導入することにします。この時、これらのパラメータの値を設計者が恣意的に決定すれば、現実に即した快適度を評価する関数とはなりません。現実にフィットした評価関数とするためには、快・不快を測定した実験データ、アンケートデータなどを用いてキャリブレーション（パラメータ推定）を行う必要があります。

☆4──［堀川］評価関数がつくられる過程に興味がある。

fig.1-1──目的関数（評価関数）とは［画像をクリックして拡大］

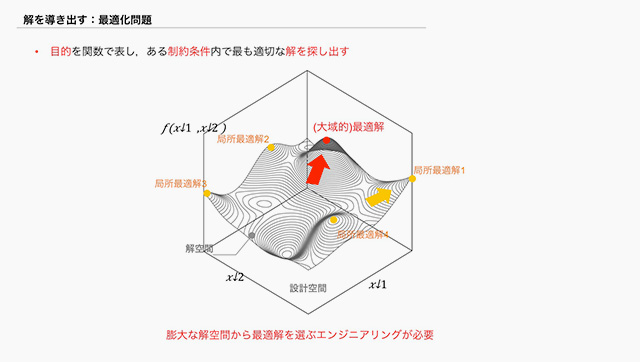
快適度の評価関数を設計したあとは、最適解を選ぶことが必要になります。具体的には、解空間（＝ありうるデザインの集合）の山を登るアルゴリズムを考え、評価が高くなるポイントを徐々に探していくことになりますが、ある山の頂上が解空間全体のなかで最もいい解だという保証はどこにもありません。複数の局所最適解があるかもしれないからです。大域的な最適解を見つけるためには、ここでもエンジニアリングが必要になります☆5［fig.1-2］。

☆5──［豊田］こうしたランドスケープダイアグラム（もちろんより高次元のものも含む）で局所最適と大域最適やその差が持つ意味は、デザインやそのほかの領域でも共有されてほしい。

fig.1-2──膨大な解空間から最適解を選ぶ［画像をクリックして拡大］

このような「目的関数のデザイン」と「解を導き出すためのエンジニアリング」、この2つを融合したデザイン・アプローチを、私は「エンジニアド・デザイン」と呼んでいます☆6。ところが、建築意匠の場合、最初の目的関数（評価関数）の設計が非常に難しいのが現状です。なぜなら、構造や環境の分野であれば、安全性や経済性、省エネルギー性といった共有しやすい指標がありますが、建築設計の場合は、誰もが共有できる指標がさまざまであり、問題が複雑になりがちだからです。

☆6──［池田］「デザイン」という概念にも多様な広がりがあるなかで、計算可能な方法論の領域に限定することにはなりますが、もちろん情報論的には最も大きな意義があります。［石澤］「目的関数をデザインする」という部分の理解は、コンピュテーショナルデザインがアルゴリズミックデザインと呼ばれていた少し前からすでにさまざまに乖離していたと思う。目的関数が出してくる形がかっこいいかどうか、という観点で考える人をいまだによく見るが、関数が説明する範囲と、それが解決する問題の範囲のマッチングをどう取り持つかには大きな責任が伴う。これに対して積極的なデザインを行わないコンピュテーショナルデザインは虚しい。

でも、都市という巨視的なスケールでは、建築の個別の問題はほぼ無視できることがあります☆7。今日は建築におけるエンジニアド・デザインの話ですが、その前に、都市解析の分野ではどのように目的関数が設定され、解が選び出されているのかについて、まずは本間さんにお話しいただきたいと思います。

☆7──［豊田］建築という領域に不可避的に潜む、複雑で複合的な評価関数の混在というリアリティと、巨視的に考えることで個別の要素が単純化されて諸々をキャンセルできる可能性。その理解が共有されない限り、言葉だけで「AIの実装」と言っても難しい。［石澤］本当にその通りだと思う。処理的に取り扱い可能にするという意味での「モデル化」という言葉も、特に建築意匠の人たちのあいだではなかなか流通していない。都市はモデル化手法に費やしてきたリソースがとても大きいけれど、建築は構造・設備に比べて建築意匠を「モデル化≒模式化」する試みが薄く、それが意匠の取り扱いにくさを生んでいる。

1.2. 本間プレゼンテーション

本間健太郎──僕は建築学の出身で、現在は東京大学空間情報科学研究センターで研究をしてします。長らく大学に在籍していて、研究もしつつ、大学の施設の設計といった実務も行っています。その経験から、「研究（エンジニアリング）と設計（デザイン）を融合したい」という強い問題意識があります。

本間健太郎氏

さて、まず都市解析の話をします。都市解析のひとつの王道が「施設配置問題」です。奈良県の図を例にお話ししましょう［fig.1-3］。慶應義塾大学の田中健一先生いわく、奈良県は人口集中地と過疎地の差がはげしく、分析手法の特性が表れやすいため、都市解析業界では奈良県をよく例にとるようです。それにならっています。この図では、39ある市町村それぞれの役場の位置をプロットしていて、円の大きさが市町村の人口を表しています。単純化して、それぞれの役場の位置に、それぞれの市町村の全住民が集まった住宅地があると考えます。このとき、39の円、つまり39の住宅地から見て、どこからも近い便利な場所に「施設」をひとつ建てたい。僕らの目的はその場所を見つけることです。これが一番シンプルな施設配置問題です。なお、ここでいう「施設」は業界用語でして、図書館や消防署などの公共施設だけでなく、大病院やドクターヘリのヘリポートなども意味しています。

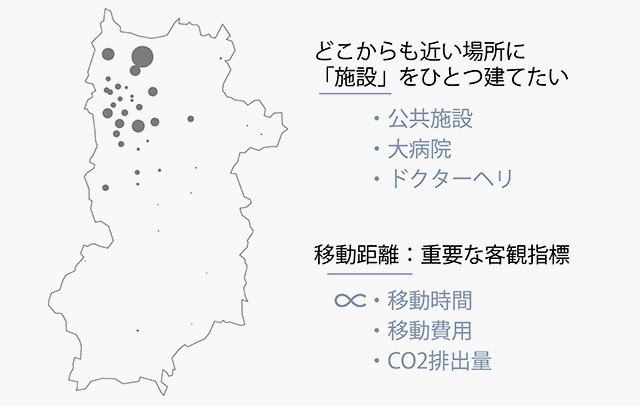
fig.1-3──施設配置問題の例

「どこからも近い」場所を見つける第一段階は、出発地から施設までの「移動距離」を測ることです。都市解析では「移動距離」がきわめて重要な客観指標です。というのも、移動距離は、移動にかかる時間や費用、ひいてはCO2排出量などに、おおよそ比例するからです。ですので、移動距離をできるだけミニマムにしたいというのは自然な要請ですね。新井さんの話になぞらえると、目的関数が移動距離だということです。それを最小化します。

ここで難儀なのが、住宅地はあちこちにあることです。ですので「施設をある住宅地に近づけたら、別の住宅地からは遠ざかる」ことが起こりえます。つまり移動距離のトレードオフがある。これをどのように調停するかが論点となります。それを考えるにあたって、2つの有名な基準があります。

ひとつは「ミニサム基準」です［fig.1-4］。この基準では、すべての住宅地から施設までの「移動距離の和」を目的関数にします。これを最小化するような、施設の立地点を見つけたいわけです。実際に計算してみると、その答えは図の赤い点になります。なお、住宅地の人口にバラツキがあるので、それぞれの人口で移動距離に「重み」をつけています。また、住宅地と施設の間の移動距離は、その直線距離と比例していると近似しています。実務では、道路や鉄道のネットワークをモデルに組み込んで計算しますが、答えはあまり変わりません。

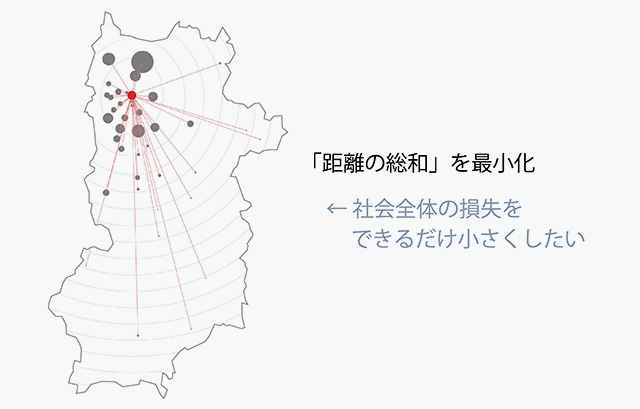
fig.1-4──ミニサム基準

図の赤いミニサム点は、北部の人口が集まっているところにあります。赤い直線が、それぞれの住宅地と施設を結んでいます。この長さを円の面積で重みをつけて、そのすべての和を考える。それを一番短くするのが、この赤い点の位置だというわけです。このように人口の多い住宅地が優先されます。ですので、施設まで極端に遠い住宅地があったとしても、その住民数が少なければ、あまり重視されません。これは不公平だという立場も十分にあり得ます。

そこで出てくるのが、もうひとつの「ミニマックス基準」です［fig.1-5］。さきほどのミニサムは、サム（合計値）をミニマイズ（最小化する）という意味です。かたやミニマックスはマックス（最大値）をミニマイズ（最小化する）ということ。この基準での目的関数は、「移動距離の最大値」、つまり最も遠い住宅地から施設までの距離です。これを最小化する。まとめると「最大値を最小化」する。ちょっと込み入った考えですね。このように、施設までの距離が最も遠い住宅地をできるだけケアするという基準なので、公平であるべき施設の配置に使われます。消防署や、ドクターヘリのヘリポートなどです。図の赤い点がミニマックス点です。県中央部にあります。ミニサム点よりだいぶ南にあるのは、南部の過疎地域に引っ張られているからです。

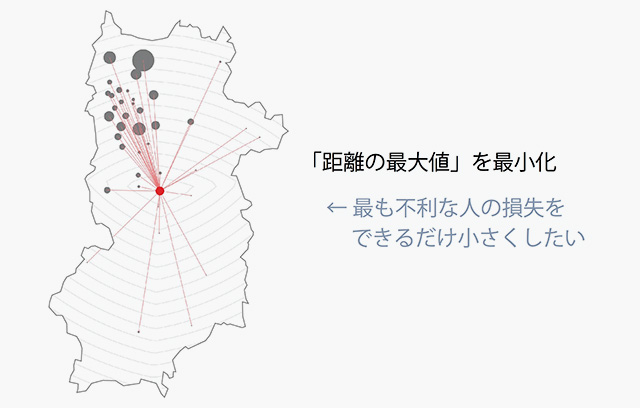
fig.1-5──ミニマックス基準

先ほど言ったように、ひとつ目のミニサム基準では「移動距離の和」を短くしようとします。では、この基準はどのような価値観に基づいているでしょうか。それは、移動にかかる時間や費用や環境負荷などについて、「社会全体での損失をできるだけ小さくしたい」という価値観です。つまり総量を問題にしている。これに対し、ミニマックス基準では、「移動距離の最大値」を短くしようとします。これは、「最も不利な人の損失をできるだけ小さくしたい」という価値観に基づいています。つまり公平性を問題にしている。

じつは、ミニサムとミニマックスは、統一してひとつの数式で表すことができます。そのような数式は無数に挙げられまして、例えばこのように表せます［fig.1-6］。この数式じたいはご理解いただかなくてよいですが、数式がパラメータをひとつ持っていることに着目してください。そのパラメータをpと呼びましょう。p＝1とおくと「ミニサム問題」になります。一方でpを無限大に近づけると「ミニマックス問題」に近づいていくのです。するとその間を考えたくなりますよね。例えばp＝2とおいたうえで最適点を計算してみましょう。すると、ミニサム問題の解（北部の点）と、ミニマックス問題の解（中部の点）の間くらいの点が求まります☆8。ちなみにこの点は人口の重心を表しています。もちろんp＝2ではなくて、5や10でもいいわけです。では逆に、pを1より小さくしたらどうなるか。pをゼロに近づけていくと、最適点は、人口が最大の住宅地に近づいていきます。このように、いろいろなpに対応する最適な地点を求められます。

☆8──［堀川］MaaSのようなモビリティのサービスの変化によって今後評価関数も変化するのだろう。

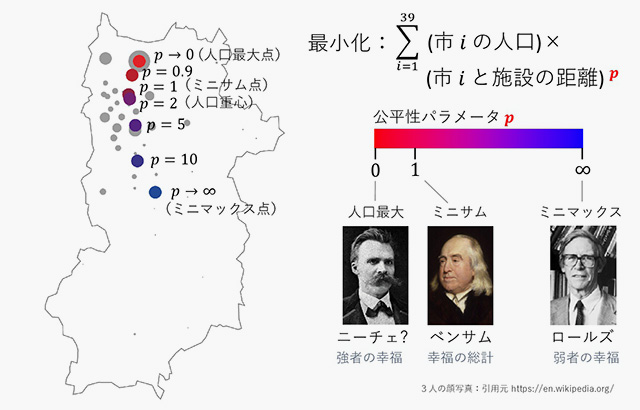
fig.1-6──ミニサムとミニマックスの統一表現

このときパラメータｐは「公平性」を表していると解釈できます。先ほど言ったように、pを1にするとミニサム問題になる。「移動距離の総和」をできるだけ短くする問題です。高校の倫理の教科書をひっぱり出してくると、これは、「幸福の総計」を最大化しようとしたベンサムの価値観に基づいていると言えます。一方でpを無限大にすると、ミニマックス問題になる。こんどは「移動距離の最大値」をできるだけ短くする問題です。この最適解は、「弱者の幸福」を高めようとしたロールズが同意してくれるでしょう。ひるがえってpをゼロにすると、最適点は人口最大点に一致する。これは、強者の側に立ったニーチェの考えと、もしかすると合うかもしれません。これは怒られるでしょうが（笑）。

このように、公平性パラメータpをいくつにするか決めるのは、価値観や倫理観であり、工学の外にあります。ここが強調したいところです。数理モデルだけで自動的に最適点が定まるわけではなく、住民や政策決定者など、だれかがpを決める必要がある。ですが、「pを決めさえすれば最適点が定まる」という枠組みを工学が提供してくれるわけです☆9。

☆9──［池田］政策的な幸福論がひとつのパラメーターでモデル化できてしまう切れ味に魅力を感じる。たとえこの対応が正しくなくとも、このモデルから思考を相対化して、新たな方向へ発展することができる。［木内］逆に言えば、手続きを徹底的に説明しきれるデザインが生み出す世界では、「事実そのように感じられる」というレベルと「そのような考え方に則っている（と知っている）」というレベルがいつも混ざって存在していて、そこでの設計は、受け手側のそうした認識の成り立ちに介入し、コミュニケーションするということでもある。考えてみれば当たり前のことだが、冒頭の定義でもあった「再現性」により、その事実が先鋭化するということに非常に面白さを感じる。

今お話ししたのが、最もシンプルな施設配置問題でした。シンプルなので抽象的な議論をするのには適していますが、そのまま現実に適用するのは無理があります。ですので、これをいろいろな方法で拡張して、現実の問題を扱えるようにするための研究が進んでいます［fig.1-7］。

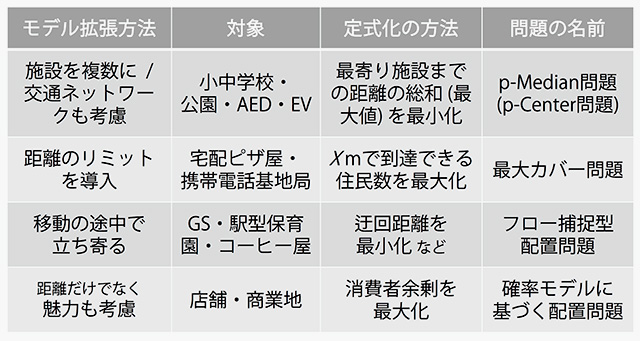
fig.1-7──施設配置問題のバリエーション

まずは配置する施設をひとつではなく複数にする拡張があります。また道路や鉄道のネットワークをモデルに組み込む拡張もたくさんあります。あるいは、例えば「30分で到達できる住民数を最大にする施設配置」を解く場合もあります。これは宅配ピザ屋の配置問題ですね。これらとは別に、「移動の途中で立ち寄る」行動に着目する研究も進んでいます。ガソリンスタンドのような立ち寄り型の施設の配置問題です。さらに、距離だけではなく、施設の魅力も考慮するモデルもあります。店の床面積や品揃えを組み込むわけです。このようなかたちで、施設配置問題はひとつの研究分野をつくっています☆10。

☆10──［堀川］データセンターのように、移動距離よりもセキュリティとインフラが重要視されるような配置問題も多くありそう。［石澤］オンラインだとパスの物理的距離よりも、その通過時に経験される上記のような属性が重要なので、マップのモデル化が変わる。交通手段によって変形する時間距離日本地図みたいな。逆にそれを建築の考え方に応用することもできそう。

新井──ありがとうございます。市川さんも距離に着目した指標で、さまざまな都市の解析をされています。どのようなアプローチをされているのでしょうか。

1.3. 市川プレゼンテーション

市川創太──私は小さな設計事務所を主宰しながら、パートナーと一緒に都市・建築を解析するソフトをつくったり、コンサルティングを行っています。先ほど本間さんがお話しされたようなセオリーなどを、どうやって実務にアプライするかに注力しています。

市川創太氏

新井さんと協働している都市研究室hclab.では、ビジュアライズの仕事から始めました。例えば、上野のある出発基点（赤い点）からそれぞれの場所に到達する「時間」をもとに描いた「時間変形地図」です［fig.1-8］。徒歩の場合と公共交通を含めた場合を比べてみると、公共交通がどれぐらい都市を縮めているのかがビジュアライズによってわかります。同様の技術を使って、交差点の通過媒介度の調査が可能です。主要駅からとある場所に人が移動するとき、最短の経路だけではなく、ふらっと通るような道も考慮した媒介度です。人が通る確率の高い交差点はどこかを計測することができます。

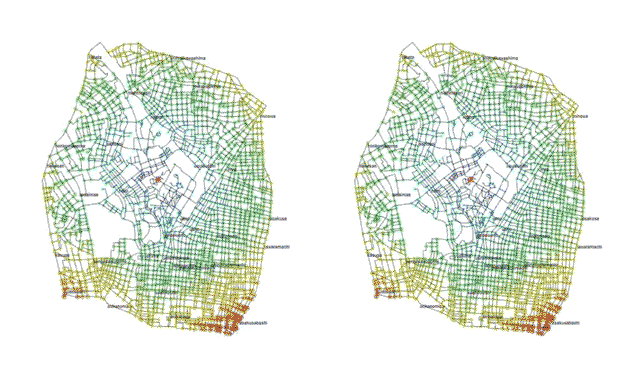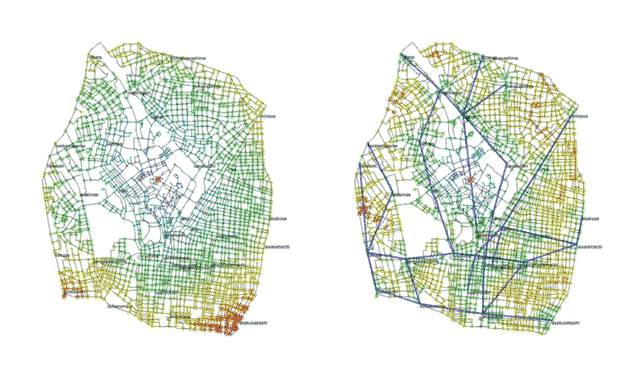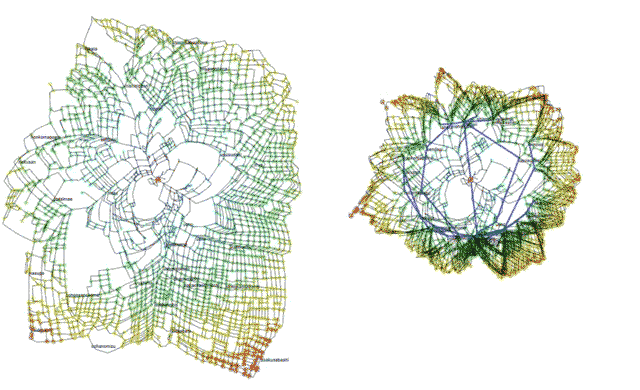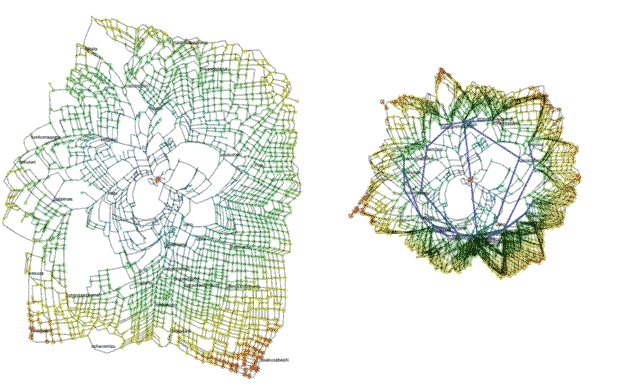
fig.1-8──上野の時間変形地図

買い物代行のベンチャー企業が使う、デリバリーシステムのプロジェクトです［fig.1-9］。買物を代行する配達員が、すべての品物をピックアップして配達までに掛かる時間をシミュレートしています。配達員がひとりの場合、複数人で分担した場合、中継した場合など、効率化のためのいくつかの配送モデルをつくり比較して、コンサルティングを行なっています。これらは、先ほどのミニサム問題や最短経路など、距離の問題への応用と言えます。

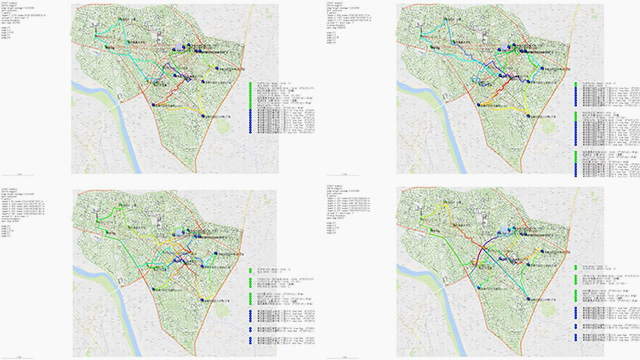
fig.1-9──デリバリーシステムのシミュレーション

案件ごとにソフトをつくりますが、毎回ゼロからつくるとすごくコストがかかってしまうので、基本的なコアの部分をあらかじめつくり、それをプロジェクトごとにカスタマイズしていくようなかたちで業務をすすめています☆11。主に「StreetView」というソフトを使っています。Goole Mapsの「Street View」とは非て非なるものです。このソフトは、CADで入力した街路のネットワークから最短経路を算出したり、ネットワーク上の時間距離を測ったりすることができます。最短経路だけではなく、最短から上位20番目までの経路を出したり媒介度を計算したり、一方通行路を考慮した経路も考慮することができます。もちろん、これらはカーナビやGoogle Mapsなどでもできますが、膨大な計算の回数が必要になる場合、GoogleのAPIではコストが合わないので、自前でつくって使用しています。無償のアカデミックバージョンがダウンロードできますので、気になる方はhclab.のウェブサイトを参照ください。

☆11──［石澤］これが大きな組織だととても難しい。解法の確立していないものは特に。リソースはあるはずだけど、誰でもサッと使えるようにするには下ごしらえの程度が整っていないといけない。

このソフトをカスタマイズしながら行った仕事のひとつが、青梅市の商工会議所の案件です。街中に増える空き店舗を活用したい、商工会議所が所有する駐車場の稼働率を上げたい、という要請がありました。空き店舗活用に向けて、事業者の誘致活動やデザインの改良といったさまざまな工夫をされていますが、そうした活動を裏打ちするために、数理的に街の店舗のポテンシャルを評価しました。

まずは技術的なお話をします。街中にある空き店舗（青い丸）があるとして、ここへ至る街全体からの経路（赤い線）をすべて合計すると、すべての場所からのそこまでの距離の総和（サム）がわかります［fig.1-10］。これは、先ほどのミニサム問題です。また、街に一様に人口が分布しているわけではないので、どこにどれぐらい人がいるかを定義します。実データがなかったので、建物の床面積にどれくらい人がいるのかを定義し、そこから割り戻して、各点ごとに人口の重みを加えました［fig.1-11］。また、対象エリア外の人口分布も考慮したうえで、徒歩や公共交通を使って利便性のいいところをヒートマップで示します。すると、赤く示されている場所がもっとも移動距離の総和が小さい便利な場所だとわかります。公共交通を使う場合と、車を使う場合とでは結果も変わります［fig.1-12］。実際の業務では、空き店舗の位置をそれぞれプロットして、同様に、人口分布の重みを考慮した利便性などの数値を計って、ランキングを出したりしています。

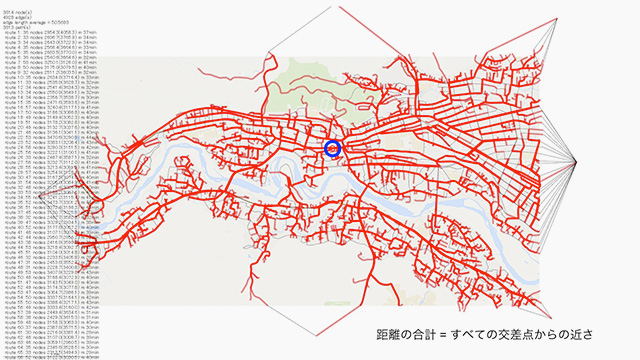
fig.1-10──街路の距離の合計（すべての交差点からの近さ）を出す

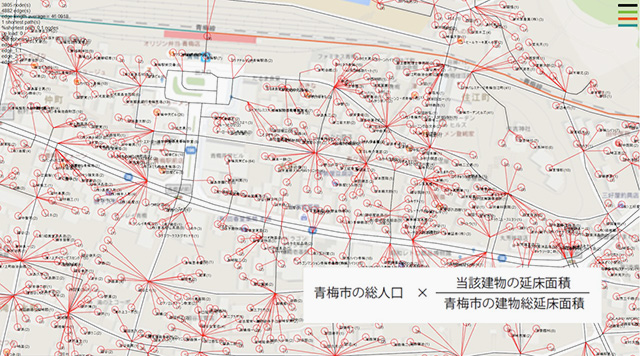
fig.1-11──各建物の床面積から、各建物に居るであろう人数を割り戻し、その人数を最寄の交差点に割り当てる

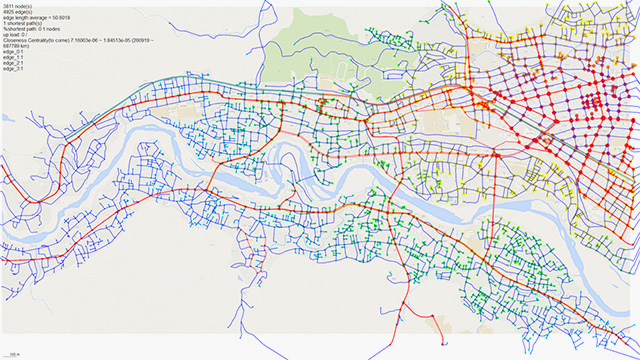
fig.1-12──自動車アクセスのヒートマップ（赤いほど利便性が高い）

店舗から駐車場までのアクセシビリティの評価も行いました。店舗から一番近い駐車場に寄って、もし満車だったら次に近い駐車場に寄り、さらにそこも満車だったら次に......と繰り返していきます。車が停められる確率は、駐車場のキャパシティによって変わります。駐車できたら、さらに徒歩で店舗までの移動します。このように、車と徒歩移動の所要時間を合計することで、それぞれの店舗の駐車場の利用のしやすさを定量的に測りました。

最終的な結果はこのようなグラフで示します［fig.1-13］。横軸が徒歩の距離で、縦軸は自動車の距離です。そして円が小さいほど駐車場が利用しやすい（時間がかからない）。なので、グラフの左下に寄っていて、かつ円が小さい場所がもっとも便利ということになりますが、実際にはすべて高評価になる店舗はありませんでした。ただし、例えば徒歩／車それぞれにとって利便性の高いエリアは異なるので、テナントの種類に応じたレコメンドや街の活性化の予測を行うことができます。

fig.1-13──青梅市内の空き店舗の評価結果［画像をクリックして拡大］